Равные комплексные числа. Действия над комплексными числами в алгебраической форме
Рассмотрим квадратное уравнение .
Определим его корни .
Не существует действительного
числа, квадрат которого равен -1. Но если формулой определить
оператор i
как мнимую единицу, то решение этого уравнения можно записать
в виде ![]() . При этом
. При этом ![]() и
и
![]() - комплексные числа, в которых -1
это действительная часть, 2 или во втором случае -2 – мнимая часть. Мнимая
часть – это также действительное (вещественное) число. Мнимая часть,
умноженная на мнимую единицу, означает уже мнимое число
.
- комплексные числа, в которых -1
это действительная часть, 2 или во втором случае -2 – мнимая часть. Мнимая
часть – это также действительное (вещественное) число. Мнимая часть,
умноженная на мнимую единицу, означает уже мнимое число
.
В общем виде комплексное число имеет вид
z = x + iy ,
где x, y – вещественные числа, – мнимая единица. В ряде прикладных наук, например, в электротехнике, электронике, теории сигналов мнимая единица обозначается через j . Вещественные числа x = Re{z} и y = Im{ z} называются вещественной и мнимой частями числа z. Выражение называется алгебраической формой записи комплексного числа.
Любое
действительное число есть частный случай комплексного числа в виде ![]() . Мнимое число тоже частный случай
комплексного числа
. Мнимое число тоже частный случай
комплексного числа ![]() .
.
Определение множества комплексных чисел С
Это выражение читается следующим образом: множество С , состоящее из элементов , таких что x и y принадлежат множеству действительных чисел R и - это мнимая единица. Отметим, что и т.д.
Два комплексных числа ![]() и
и ![]() равны, если и только если равны их
действительные и мнимые части, т.е. и .
равны, если и только если равны их
действительные и мнимые части, т.е. и .
Комплексные числа и функции широко используются в науке и технике, в частности, в механике, анализе и расчете цепей переменного тока, аналоговой электронике, в теории и обработке сигналов, в теории автоматического управления и др. прикладных науках.
- Арифметика комплексных чисел
Сложение двух комплексных чисел состоит в сложении их действительных и мнимых частей, т.е.
Соответственно разность двух комплексных чисел
Комплексное число ![]() называется
комплексно
сопряженным
числу z
=
x +
iy.
называется
комплексно
сопряженным
числу z
=
x +
iy.
Комплексно сопряженные числа z и z * отличаются знаками мнимой части. Очевидно, что
 .
.
Любое равенство между комплексными выражениями остается
справедливым, если в этом равенстве всюду i
заменить на -
i
,
т.е. перейти к равенству сопряженных чисел. Числа i
и –
i
алгебраически
неразличимы, поскольку ![]() .
.
Произведение (умножение) двух комплексных чисел может быть вычислено следующим образом:
Деление двух комплексных чисел:
Пример :
- Комплексная плоскость
Комплексное число графически можно представить в прямоугольной системе координат. Зададим в плоскости прямоугольную систему координат (x, y).
На оси Ox будем располагать действительные части x , она называется действительной (вещественной) осью , на оси Oy –мнимые части y комплексных чисел. Она носит название мнимой оси . При этом каждому комплексному числу соответствует определенная точка плоскости, и такая плоскость называется комплексной плоскостью . Точке А комплексной плоскости будет соответствовать вектор ОА .
Число x называется абсциссой комплексного числа , число y – ординатой .
Пара комплексно сопряженных чисел отображается точками, расположенными симметрично относительно действительной оси.
 |
Если на плоскости задать полярную
систему координат
, то каждое комплексное число z
определяется полярными координатами . При этом модуль
числа ![]() – это полярный радиус точки, а угол
– это полярный радиус точки, а угол
 - её полярный угол
или аргумент комплексного числа z
.
- её полярный угол
или аргумент комплексного числа z
.
Модуль
комплексного числа ![]() всегда неотрицательный. Аргумент комплексного числа не
определяется однозначно. Главное значение аргумента должно удовлетворять
условию
всегда неотрицательный. Аргумент комплексного числа не
определяется однозначно. Главное значение аргумента должно удовлетворять
условию ![]() . Каждой точке комплексной плоскости
соответствует также общее значение аргумента .
Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент
числа нуль не определен.
. Каждой точке комплексной плоскости
соответствует также общее значение аргумента .
Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент
числа нуль не определен.
Главное значение аргумента определяют по выражениям:

Очевидно, что
При этом
,  .
.
Представление комплексного числа z в виде
называется тригонометрической формой комплексного числа.
Пример .
![]()
- Показательная форма комплексных чисел
Разложение в ряд Маклорена
для функций действительного аргумента ![]() имеет
вид:
имеет
вид:

Для экспоненциальной функции комплексного аргумента z разложение имеет аналогичный характер
 .
.
Разложение в ряд Маклорена для экспоненциальной функции мнимого аргумента можно представить как

Получившееся тождество называется формулой Эйлера .
Для отрицательного аргумента оно имеет вид
Комбинируя эти выражения, можно определить следующие выражения для синуса и косинуса
 .
.
Пользуясь формулой Эйлера, из тригонометрической формы представления комплексных чисел
можно получить показательную (экспоненциальную, полярную) форму комплексного числа, т.е. его представление в виде
![]() ,
,
где ![]() - полярные
координаты точки с прямоугольными координатами (x,
y
).
- полярные
координаты точки с прямоугольными координатами (x,
y
).
Число, сопряженное комплексному числу , в показательной форме записывается следующим образом .
Для показательной формы легко определить следующие формулы умножения и деления комплексных чисел

Т.е., в показательной форме произведение и деление комплексных чисел выполняется проще, чем в алгебраической форме. При умножении модули сомножителей перемножаются, а аргументы складываются. Это правило распространяется на любое число сомножителей. В частности, при умножении комплексного числа z на i вектор z поворачивается против часовой стрелки на 90
При делении модуль числителя делится на модуль знаменателя, и из аргумента числителя вычитается аргумент знаменателя.
Используя показательную форму комплексных чисел, можно получить выражения для известных тригонометрических тождеств. Например, из тождества
![]()
с помощью формулы Эйлера можно записать
Приравнивая действительную и мнимую части в данном выражении, получаем выражения для косинуса и синуса суммы углов
- Степени, корни и логарифмы комплексных чисел
Возведение комплексного числа в натуральную степень n производится по формуле
Пример
. Вычислим ![]() .
.
Представим число ![]() в тригонометрической форме
в тригонометрической форме
 ’
’
Применяя формулу возведения в степень, получим
Положив в выражении значение r = 1, получим так называемую формулу Муавра , при помощи которой можно определять выражения синусов и косинусов кратных углов.
Корень n –й степени из комплексного числа z имеет n различных значений, определяемых по выражению
Пример . Найдем .
Для этого выразим комплексное число () к тригонометрической форме
 .
.
По формуле вычисления корня из комплексного числа, получаем
Логарифм комплексного числа z – это число w , для которого . Натуральный логарифм комплексного числа имеет бесконечное множество значений и вычисляется по формуле
Состоит из действительной (косинусоидальной) и мнимой (синусоидальной) части. Такое напряжение можно представлять как вектор длиной U m , начальной фазой (углом) , вращающийся с угловой скоростью ω .

При этом если комплексные функции складываются, то складываются их вещественные и мнимые части. Если комплексная функция умножается на константу или вещественную функцию, то её вещественная и мнимая части умножаются на тот же множитель. Дифференцирование / интегрирование такой комплексной функции сводится к дифференцированию / интегрированию вещественной и мнимой части.
Например, дифференцирование выражения комплексного напряжения
 заключается
в умножении его на iω
- вещественная часть функции f(z),
а
заключается
в умножении его на iω
- вещественная часть функции f(z),
а ![]() – мнимая часть функции. Примеры:
– мнимая часть функции. Примеры:  .
.
Значение z изображается точкой в комплексной плоскости z, а соответствующее значение w - точкой в комплексной плоскости w . При отображении w = f(z) линии плоскости z переходят в линии плоскости w , фигуры одной плоскости в фигуры другой, но формы линий или фигур могут существенно измениться.
Комплексные числа - расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма , где и - вещественные числа, - мнимая единица.
Запись комплексного числа в виде , , называется алгебраической формой комплексного числа.
Свойства комплексных чисел. Геометрическая интерпретация комплексного числа.
Действия над комплексными числами, заданными в алгебраической форме:
Рассмотрим правила, по которым производятся арифметические действия над комплексными числами.
Если даны два комплексных числа α = a + bi и β = c + di, то
α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,
α – β = (a + bi) – (c + di) = (a – c) + (b – d)i . (11)
Это следует из определения действий сложения и вычитания двух упорядоченных пар действительных чисел (см. формулы (1) и (3)). Мы получили правила сложения и вычитания комплексных чисел: чтобы сложить два комплексных числа, надо отдельно сложить их действительные части и соответственно мнимые части; чтобы из одного комплексного числа вычесть другое, необходимо вычесть соответственно их действительные и мнимые части.
Число – α = – a – bi называют противоположным числу α = a + bi . Сумма двух этих чисел равна нулю: - α + α = (- a - bi) + (a + bi) = (-a + a) + (-b + b)i = 0.
Для получения правила умножения комплексных чисел воспользуемся формулой (6), т. е. тем, что i2 = -1. Учитывая это соотношение, находим (a + bi)(c + di) = ac + adi + bci + bdi2 = ac + (ad + bc)i – bd, т.е.
(a + bi)(c + di) = (ac - bd) + (ad + bc)i . (12)
Эта формула соответствует формуле (2), которой определялось умножение упорядоченных пар действительных чисел.
Отметим, что сумма и произведение двух комплексно сопряженных чисел являются действительными числами. Всамомделе, еслиα = a + bi, = a – bi, тоα = (a + bi)(a - bi) = a2 – i2b2 = a2 + b2 , α + = (a + bi) + (a - bi) = (a + a) + (b - b)i= 2a, т.е.
α + = 2a, α = a2 + b2. (13)
При делении двух комплексных чисел в алгебраической форме следует ожидать, что частное выражается также числом того же вида, т. е. α/β = u + vi, где u, v R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + bi, β = c + di, причем β ≠ 0, т. е. c2 + d2 ≠ 0. Последнее неравенство означает, что c и d одновременно в нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу (12) и второе из равенств (13), находим:
Следовательно, частное двух комплексных чисел определяется формулой:
соответствующей формуле (4).
С помощью полученной формулы для числа β = с + di можно найти обратное ему число β-1 = 1/β. Полагая в формуле (14) а = 1, b = 0, получаем
Эта формула определяет число, обратное данному комплексному числу, отличному от нуля; это число также является комплексным.
Например: (3 + 7i) + (4 + 2i) = 7 + 9i;
(6 + 5i) – (3 + 8i) = 3 – 3i;
(5 – 4i)(8 – 9i) = 4 – 77i;
Действия над комплексными числами в алгебраической форме.

55. Аргумент комплексного числа. Тригонометрическая форма записи комплексного числа (вывод).
Арг.ком.числа. – между положительным направлением действительной оси Х вектором изображающим данное число.
Формула тригон. Числа: ,
Комплексные числа
Мнимые и комплексные числа. Абсцисса и ордината
комплексного числа. Сопряжённые комплексные числа.
Операции с комплексными числами. Геометрическое
представление комплексных чисел. Комплексная плоскость.
Модуль и аргумент комплексного числа. Тригонометрическая
форма комплексного числа. Операции с комплексными
числами в тригонометрической форме. Формула Муавра.
Начальные сведения о мнимых и комплексных числах приведены в разделе «Мнимые и комплексные числа». Необходимость в этих числах нового типа появилась при решении квадратных уравнений для случая
D < 0 (здесь D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физикии техники: электротехнике, гидро- и аэродинамике, теории упругости и др.
Комплексные числа записываются в виде: a + bi . Здесь a и b – действительные числа , а i – мнимая единица, т. e . i 2 = –1. Число a называется абсциссой , a b – ординатой комплексного числа a + bi . Два комплексных числа a + bi и a – bi называются сопряжёнными комплексными числами.
Основные договорённости:
1. Действительное число
а может быть также записано в форме комплексного числа: a + 0 i или a – 0 i . Например, записи 5 + 0 i и 5 – 0 i означают одно и то же число 5 .2. Комплексное число 0+ bi называется чисто мнимым числом . Запись bi означает то же самое, что и 0+ bi .
3. Два комплексных числа a + bi и c + di считаются равными, если a = c и b = d . В противном случае комплексные числа не равны.
Сложение. Суммой комплексных чисел a + bi и c + di называется комплексное число (a + c ) + (b + d ) i . Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.
Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое) называется комплексное число ( a – c ) + (b – d ) i .
Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a + bi и c + di называется комплексное число:
( ac – bd ) + (ad + bc ) i . Это определение вытекает из двух требований:
1) числа a + bi и c + di должны перемножаться, как алгебраические двучлены,
2) число i обладает основным свойством: i 2 = – 1.
П р и м е р . (a+ bi )( a – bi ) = a 2 + b 2 . Следовательно, произведение
двух сопряжённых комплексных чисел равно действительному
положительному числу.
Деление. Разделить комплексное число a + bi (делимое) на другое c + di (делитель) - значит найти третье число e + f i (чатное), которое будучи умноженным на делитель c + di , даёт в результате делимое a + bi .
Если делитель не равен нулю, деление всегда возможно.
П р и м е р. Найти (8 + i ) : (2 – 3 i ) .
Р е ш е н и е. Перепишем это отношение в виде дроби:
Умножив её числитель и знаменатель на 2 + 3 i
И выполнив все преобразования, получим:
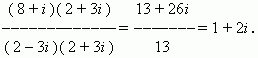
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a + bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью .

Модулем комплексного числа называется длина вектора OP , изображающего комплексное число на координатной (комплексной ) плоскости. Модуль комплексного числа a + bi обозначается | a + bi | или буквой r
Алгебраическая форма записи комплексного числа................................................................ |
|||
Плоскость комплексных чисел.................................................................................................... |
|||
Комплексно сопряжённые числа................................................................................................. |
|||
Действия с комплексными числами в алгебраической форме............................................... |
|||
Сложение комплексных чисел................................................................................................. |
|||
Вычитание комплексных чисел............................................................................................... |
|||
Умножение комплексных чисел.............................................................................................. |
|||
Деление комплексных чисел.................................................................................................... |
|||
Тригонометрическая форма записи комплексного числа....................................................... |
|||
Действия с комплексными числами в тригонометрической форме...................................... |
|||
Умножение комплексных чисел в тригонометрической форме......................................... |
|||
Деление комплексных чисел в тригонометрической форме............................................... |
|||
Возведение комплексного числа в целую положительную степень.................................. |
|||
Извлечение корня целой положительной степени из комплексного числа..................... |
|||
Возведение комплексного числа в рациональную степень................................................. |
|||
Комплексные ряды...................................................................................................................... |
|||
Комплексные числовые ряды................................................................................................. |
|||
Степенные ряды в комплексной плоскости......................................................................... |
|||
Двусторонние степенные ряды в комплексной плоскости............................................... |
|||
Функции комплексного переменного....................................................................................... |
|||
Основные элементарные функции........................................................................................ |
|||
Формулы Эйлера...................................................................................................................... |
|||
Показательная форма представления комплексного числа.............................................. |
|||
Связь между тригонометрическими и гиперболическими функциями.......................... |
|||
Логарифмическая функция..................................................................................................... |
|||
Общая показательная и общая степенная функции........................................................... |
|||
Дифференцирование функций комплексного переменного................................................. |
|||
Условия Коши-Римана............................................................................................................ |
|||
Формулы для вычисления производной............................................................................... |
|||
Свойства операции дифференцирования............................................................................. |
|||
Свойства действительной и мнимой частей аналитической функции............................ |
|||
Восстановление функции комплексного переменного по её действительной или мнимой |
|||
Способ №1. С помощью криволинейного интеграла..................................................... |
|||
Способ №2. Непосредственное применение условий Коши-Римана.......................... |
|||
Способ №3. Через производную искомой функции....................................................... |
|||
Интегрирование функций комплексного переменного......................................................... |
|||
Интегральная формула Коши.................................................................................................... |
|||
Разложение функций в ряды Тейлора и Лорана..................................................................... |
|||
Нули и особые точки функции комплексного переменного................................................ |
|||
Нули функции комплексного переменного..................................................................... |
|||
Изолированные особые точки функции комплексного переменного......................... |
|||
14.3 Бесконечно удалённая точка как особая точка функции комплексного переменного
Вычеты........................................................................................................................................... |
|||
Вычет в конечной точке...................................................................................................... |
|||
Вычет функции в бесконечно удаленной точке.............................................................. |
|||
Вычисление интегралов с помощью вычетов......................................................................... |
|||
Вопросы для самопроверки........................................................................................................ |
|||
Литература.................................................................................................................................... |
|||
Предметный указатель................................................................................................................ |
|||
Предисловие
Правильно распределить время и силы при подготовке к теоретической и практической частям экзамена или аттестации по модулю достаточно сложно, тем более что в период сессии времени всегда не хватает. И как показывает практика, справиться с этим получается не у всех. В результате на экзамене одни студенты правильно решают задачи, но затрудняются ответить на простейшие теоретические вопросы, а другие могут сформулировать теорему, но не могут её применить.
Настоящие методические рекомендации для подготовки к экзамену по курсу «Теория функций комплексного переменного» (ТФКП) являются попыткой разрешить это противоречие и обеспечить одновременное повторение теоретического и практического материала курса. Руководствуясь принципом «Теория без практики мертва, практика без теории слепа», они содержат как теоретические положения курса на уровне определений и формулировок, так и примеры, иллюстрирующие применение каждого приведенного теоретического положения, и, тем самым, облегчающие его запоминание и понимание.
Цель предлагаемых методических рекомендаций – помочь студенту подготовиться к экзамену на базовом уровне. Иными словами, составлен расширенный рабочий справочник, содержащий основные моменты, используемые на занятиях по курсу ТФКП, и необходимые при выполнении домашнего задания и подготовке к контрольным мероприятиям. Помимо самостоятельной работы студентов, настоящее электронное учебное издание можно использовать при проведении занятий в интерактивной форме с использованием электронной доски или для размещения в системе дистанционного обучения.
Обращаем внимание, что настоящий труд не заменяет собой ни учебников, ни конспекта лекций. Для углублённого изучения материала рекомендуется обращаться к соответствующим разделам изданного в МГТУ им. Н.Э. Баумана базового учебника .
В конце пособия помещён список рекомендуемой литературы и предметный указатель, в который входят все выделенные в текстеполужирным курсивом термины. Предметный указатель состоит из гиперссылок на разделы, в которых эти термины строго определены или описаны и где приведены примеры, иллюстрирующие их применение.
Пособие предназначено для студентов 2 курса всех факультетов МГТУ им. Н.Э. Баумана.

1. Алгебраическая форма записи комплексного числа
Запись вида z = x + iy , где x , y - действительные числа, i - мнимая единица (т.е. i 2 = − 1)
называют алгебраической формой записи комплексного числа z. При этом x называют действительной частью комплексного числа и обозначают Re z (x = Re z ), y называют мнимой частью комплексного числа и обозначают Im z (y = Im z ).
Пример. У комплексного числа z = 4 − 3i действительная часть Re z = 4 , а мнимая Im z = − 3 .
2. Плоскость комплексных чисел
В теории функций комплексного переменного рассматривают плоскость комплексных чисел , которую обозначают либо, либо используют буквы, обозначающие комплексные числа z , w и т.п.
Горизонтальная ось комплексной плоскости называется действительной осью , на ней располагают действительные числа z = x + 0 i = x .
Вертикальная ось комплексной плоскости называется мнимой осью , на ней располагают
3. Комплексно сопряжённые числа
Числа z = x + iy и z = x − iy называют комплексно сопряжёнными . На комплексной плоскости им соответствуют точки, симметричные относительно действительной оси.
4. Действия с комплексными числамив алгебраической форме
4.1 Сложение комплексных чисел
Суммой двух комплексных чисел |
z 1 = x 1 + iy 1 |
и z 2 = x 2 + iy 2 называется комплексное число |
|||||||||||
z 1 + z 2 |
= (x 1 + iy 1 ) + (x 2 + iy 2 ) = (x 1 + x 2 ) + i (y 1 + y 2 ) . |
операция |
сложения |
||||||||||
комплексных чисел аналогична операции сложения алгебраических двучленов. |
|||||||||||||
Пример. Суммой двух комплексных чисел z 1 = 3 + 7i и z 2 |
= −1 +2 i |
будет комплексное число |
|||||||||||
z 1 + z 2 = (3 +7 i ) +(−1 +2 i ) = (3 −1 ) +(7 +2 ) i = 2 +9 i . |
|||||||||||||
Очевидно, |
суммой комплексно |
сопряжённых |
является |
действительное |
|||||||||
z + z = (x + iy) + (x − iy) = 2 x = 2 Re z . |
|||||||||||||
4.2 Вычитание комплексных чисел |
|||||||||||||
Разностью двух комплексных чисел z 1 = x 1 + iy 1 |
X 2 +iy 2 |
называется |
комплексное |
||||||||||
число z 1 − z 2 = (x 1 + iy 1 ) − (x 2 + iy 2 ) = (x 1 − x 2 ) + i (y 1 − y 2 ) . |
|||||||||||||
Пример. Разностью двух комплексных чисел |
z 1 = 3 −4 i |
и z 2 |
= −1 +2 i |
будет комплексное |
|||||||||
число z 1 − z 2 = (3 − 4i ) − (− 1+ 2i ) = (3 − (− 1) ) + (− 4 − 2) i = 4 − 6i . |
|||||||||||||
Разностью |
комплексно сопряжённых |
является |
|||||||||||
z − z = (x + iy) − (x − iy) = 2 iy = 2 i Im z . |
|||||||||||||
4.3 Умножение комплексных чисел |
|||||||||||||
Произведением двух комплексных чисел |
z 1 = x 1 + iy 1 |
и z 2 = x 2 + iy 2 |
называется комплексное |
||||||||||
z 1z 2 = (x 1 + iy 1 )(x 2 + iy 2 ) = x 1x 2 + iy 1x 2 + iy 2 x 1 + i 2 y 1 y 2 |
= (x 1x 2 − y 1 y 2 ) + i (y 1x 2 + y 2 x ) . |
||||||||||||
образом, операция умножения комплексных чисел аналогична операции умножения алгебраических двучленов с учётом того, что i 2 = − 1.
Напомним необходимые сведения о комплексных числах.
Комплексное число - это выражение вида a + bi , где a , b - действительные числа, а i - так называемая мнимая единица , символ, квадрат которого равен –1, то есть i 2 = –1. Число a называется действительной частью , а число b - мнимой частью комплексного числа z = a + bi . Если b = 0, то вместо a + 0i пишут просто a . Видно, что действительные числа - это частный случай комплексных чисел.
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi ) ± (c + di ) = (a ± c ) + (b ± d )i , а умножение - по правилу (a + bi ) · (c + di ) = (ac – bd ) + (ad + bc )i (здесь как раз используется, что i 2 = –1). Число = a – bi называется комплексно-сопряженным к z = a + bi . Равенство z · = a 2 + b 2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
(Например, ![]() .)
.)

У комплексных чисел есть удобное и наглядное геометрическое представление: число z
= a
+ bi
можно изображать вектором с координатами (a
; b
) на декартовой плоскости (или, что почти то же самое, точкой - концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a
; b
) равна . Эта величина называется модулем
комплексного числа z
= a
+ bi
и обозначается |z
|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом
комплексного числа z
и обозначается Arg z
. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π
радиан (или 360°, если считать в градусах) - ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r
образует угол φ
с положительным направлением оси абсцисс, то его координаты равны (r
· cos φ
; r
· sin φ
). Отсюда получается тригонометрическая форма записи
комплексного числа: z
= |z
| · (cos(Arg z
) + i
sin(Arg z
)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z
1 · z
2 = |z
1 | · |z
2 | · (cos(Arg z
1 + Arg z
2) + i
sin(Arg z
1 + Arg z
2)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра
: z n
= |z
| n
· (cos(n
· (Arg z
)) + i
sin(n
· (Arg z
))). С помощью этих формул легко научиться извлекать корни любой степени из комплексных чисел. Корень n-й степени из числа z
- это такое комплексное число w
, что w n
= z
. Видно, что ![]() , а , где k
может принимать любое значение из множества {0, 1, ..., n
– 1}. Это означает, что всегда есть ровно n
корней n
-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n
-угольника).
, а , где k
может принимать любое значение из множества {0, 1, ..., n
– 1}. Это означает, что всегда есть ровно n
корней n
-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n
-угольника).