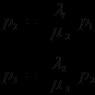Распределение больцмана частиц во внешнем поле. Закон больцмана для распределения частиц во внешнем потенциальном поле

Барометрическая формула - зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:

где p - давление газа в слое, расположенном на высоте h , p 0 - давление на нулевом уровне (h = h 0), M - молярная масса газа, R - газовая постоянная, T - абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

где M - молярная масса газа, R - газовая постоянная.

Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина , определяющая быстроту спада плотности, представляет собой отношение потенциальной энергии частиц к их средней кинетической энергии, пропорциональной kT . Чем выше температура T , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести mg (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести mg может изменяться за счёт двух величин: ускорения g и массы частиц m .

Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Пусть идеальный газ находится в поле консервативных сил в условиях теплового равновесия. При этом концентрация газа будет различной в точках с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия. Так, число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения P = nkT , падает.

Если известно число молекул в единичном объеме, то известно и давление, и наоборот. Давление и плотность пропорциональны друг другу, поскольку температура в нашем случае постоянна. Давление с уменьшением высоты должно возрастать, потому что нижнему слою приходится выдерживать вес всех расположенных сверху атомов.

Исходя из основного уравнения молекулярно-кинетической теории: P = nkT , заменим P и P 0 в барометрической формуле (2.4.1) на n и n 0 и получим распределение Больцмана для молярной массы газа:

С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При T = 0 тепловое движение прекращается, все молекулы расположились бы на земной поверхности. При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой. Так как mgh – это потенциальная энергия U , то на разных высотах U = mgh – различна. Следовательно, (2.5.2) характеризует распределение частиц по значениям потенциальной энергии:

– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n 0 – число молекул в единице объёма там, где U = 0.

Полученная в § 92 барометрическая формула

(см. (92.4)) дает зависимость давления от высоты над поверхностью Земли для воображаемой изотермической атмосферы. Заменим в показателе экспоненты отношение равным ему отношением ( - масса молекулы, k - постоянная Больцмана). Кроме того, подставим в соответствии с (86.7) вместо выражение а вместо - выражение Сократив затем обе части равенства на придем к формуле

(100.2)

Здесь - концентрация молекул (т. е. число их в единице объема) на высоте - концентрация молекул на высоте

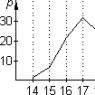
Из формулы (100.2) следует, что с понижением температуры число частиц на высотах, отличных от нуля, убывает, обращаясь в нуль при (рис. 100.1). При абсолютном нуле все молекулы расположились бы на земной поверхности.

При высоких температурах, напротив, слабо убывает с высотой, так что молекулы оказываются распределенными по высоте почти равномерно.

Этот факт имеет простое физическое объяснение. Каждое конкретное распределение молекул по высоте устанавливается в результате действия двух тенденций: 1) притяжение молекул к Земле (характеризуемое силой ) стремится расположить их на поверхности Земли; 2) тепловое движение (характеризуемое величиной ) стремится разбросать молекулы равномерно по всем высотам. Чем больше и меньше Т, тем сильнее преобладает первая тенденция, и молекулы сгущаются у поверхности Земли. В пределе при тепловое движение совсем прекращается, и под влиянием притяжения молекулы располагаются на земной поверхности. При высоких температурах превалирует тепловое движение, и плотность молекул медленно убывает с высотой.

На разной высоте молекула обладает различным запасом по тенциальной энергии:

Следовательно, распределение молекул по высоте является вместе с тем и распределением их по значениям потенциальной энергии. С учетом (100.3) формулу (100.2) можно записать следующим образом:

где - плотность молекул в том месте пространства, где потенциальная энергия молекулы имеет значение - плотность молекул в том месте, где потенциальная энергия молекулы равна нулю.

Из (100.4) следует, что молекулы располагаются с большей плотностью там, где меньше их потенциальная энергия, и, наоборот, с меньшей плотностью - в местах, где их потенциальная энергия больше.

В соответствии с (100.4) отношение в точках, где потенциальная энергия молекулы имеет значения равно

Больцман доказал, что распределение (100.4) справедливо не только в случае потенциального поля сил земного тяготения, но и в любом потенциальном поле сил для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. В соответствии с этим распределение (100.4) называют распределением Больцмана.

В то время как закон Максвелла дает распределение частиц по значениям кинетической энергии, закон Больцмана дает распределение частиц по значениям потенциальной энергии. Для обоих распределений характерно наличие экспоненциального множителя, в показателе которого стоит отношение кинетической или соответственно потенциальной энергии одной молекулы к величине, определяющей среднюю энергию теплового движения молекулы.

Согласно формуле (100.4) количество молекул, попадающих в пределы объема расположенного в точке с координатами х, у, z, равно

Мы получили еще одно выражение закона распределения Больцмана.

Распределения Максвелла и Больцмана можно объединить в один закон Максвелла - Больцмана, согласно которому число молекул, компоненты скорости которых лежат в пределах от до а координаты в пределах от х, у, z до равно

Распределение Больцмана для частиц во внешнем потенциальном поле

Газ, на который не действует внешнее силовое поле, равно­мерно заполняет объем, в котором он находится, благодаря хаотичности теплового движения молекул. Если на молекулы газа действуют внешние силы, то концентрация газа не будет одинаковой во всех точках объема. Рассмотрим в качестве примера атмосферный газ, находящийся в поле земного тяго­тения. Если бы отсутствовало тепловое движение, то все мо­лекулы атмосферы опустились бы на поверхность Земли под действием сил тяжести и земная атмосфера не могла бы суще­ствовать. Однако этому препятствует хаотическое движение молекул, которое способствует обратному процессу - стремле­нию атмосферного газа рассеяться и заполнить равномерно всю Вселенную. Следовательно, атмосфера Земли может существовать за счет этих двух факторов в некотором равновесном состоянии, при котором ее плотность, концентрация молекул и давление будут зависеть от пространственных ко­ординат.

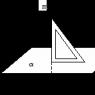
Найдем закон измене­ния этих величин в зависимости от высоты над поверхностью Земли. Бу­дем считать, что газ на­ходится в состоянии термодинамического равно­весия и его температура всюду одинакова. Выделим некоторый столб газа, имеющий форму цилиндра, площадью поперечного сече­ния s, и направим ось z вдоль столба по направлению от поверхности Земли. Установим начало отсчета координаты z на поверхности Земли (рис. 19.3).

Выделим на высоте z элементарный слой столба газа тол­щиной dz и воспользуемся тем, что этот слой, как и весь столб, находится в состоянии механического равновесия. Это значит, что равнодействующая всех сил, действующих на слой, равна нулю. Из рис. 19.3 видно, что равнодействующая складыва­ется из трех сил: две силы давления F H и F B , действующие на нижнее и верхнее основание слоя, и сила тяжести dP самого слоя. Обозначим давление газа в точках нижнего основания p , а в точках верхнего основания р+ dp. Тогда

F H = pS ; F B = (p + dp)S; dP = ρgSdz,

где ρ - плотность слоя воздуха.

С учетом направления сил условие равновесия слоя запишется в виде

F B + dP = F H (18.28)

(р + dp) S + ρgSdz = pS. (18.29)

Раскрыв в (18.29) скобки, получим дифференциальное уравнение

dp = - ρgdz. (18.30)

Из уравнения Клапейрона - Менделеева следует, что плотность газа связана с давлением формулой

где т а - масса молекулы газа.

Используя (18.31), преобразуем дифференциальное урав­нение (18.30) к виду

. (18.32)

Интегрируя это уравнение по высоте от 0 до z, получаем

, (18.33)

где ln p 0 - постоянная интегрирования.

Потенциируя (18.33), имеем

Из (18.34) видно, что р 0 имеет смысл давления атмосферы на поверхности Земли, где z = 0.

Полученное уравнение определяет зависимость давления атмосферы вблизи Земли от высоты над уровнем моря. Как и следовало ожидать, при увеличении высоты давление уменьшается. В соответствии с формулой (18.34), которая называется барометрической, это уменьшение подчиняется экспоненциальному закону. Измеряя давление по барометру, проградуированному в соответствии с барометрической фор­мулой, можно определить высоту объекта над поверхностью Земли. Такой прибор называется альтиметром и широко при­меняется в авиации.

Используя барометрическую формулу, легко установить закон распределения концентрации молекул по высоте h над поверхностью Земли. С этой целью воспользуемся уравнени­ем состояния идеального газа p= nkT. В этой формуле дав­ление р и концентрация молекул п зависят от высоты, в то время как температура Т постоянная в соответствии с пред­положением, что газ находится в состоянии термодинамиче­ского равновесия. Из уравнения состояния и барометрической формулы для концентрации п на высоте h вытекает:

, (18.35)

где n 0 - концентрация молекул воздуха при h = 0.

Обратив внимание на то, что в показатель экспоненты в правой части (18.35) входит потенциальная энергия моле­кулы в поле силы тяжести W ПОТ = m a gh, перепишем (18.35) в виде

. (18.36)

Оказывается, что выражение (18.36) для распределения молекул имеет общий характер и справедливо для частиц, находящихся во внешнем потенциальном поле любого вида. Это распределение называется распределением Больцмана.

В распределении Больцмана (18.36) под n 0 следует пони­мать концентрацию молекул в точке поля, где их потенциаль­ная энергия равна нулю, W ПОТ = 0, а п представляет собой концентрацию молекул в точке, где их потенциальная энергия равна W ПОТ.

Как известно, плотность газа ρ прямо пропорциональна концентрации молекул п. Поэтому, используя (18.35), нетруд­но показать, что распределение плотности воздуха в атмо­сфере Земли будет описываться выражением:

, (18.37)

где М - молярная масса газа.

Из (18.34), (18.35) и (18.37) следует, что в атмосфере Земли р, п и ρ воздуха уменьшаются единообразно с увели­чением высоты.

Учитывая, что концентрация п по определению равна , где dN - число молекул в элементарном объеме dV , можно представить распределение Больцмана в форме

Пусть идеальный газ находится в каком-либо силовом поле, например, в поле тяжести. Так как на молекулы газа в этом случае действуют внешние силы, то давление газа не будет всюду одинаковым, а будет меняться от точки к точке.

В простейшем случае силы поля имеют неизменное направление, характеризуемое осью z. Пусть две площадки единичной площади ориентированы перпендикулярно оси z и находятся друг от друга на расстоянии dz. Если давления газа на обеих площадках равны р и p + dp, то разность давлений должна, очевидно, равняться суммарной силе, действующей на частицы газа, заключенные в объеме параллелепипеда с единичным основанием и высотой dz . Эта сила равна Fn dz , где n – плотность молекул (т. е. их число в единице объема), a F – сила, действующая на одну молекулу в точке с координатой z . Поэтому

dp = nF dz .

Сила F связана с потенциальной энергией U(z) молекулы соотношением F = - dU/dz, так что

dp = – n dz dU /dz = – n dU .

Так как газ предполагается идеальным, то p = nkT . Если температура газа в различных точках одинакова, то

dp = kT dn .

Разность давлений dp в обоих случаях определяется разностью высот. Поэтому

и окончательно

Здесь n 0 – постоянная, представляющая собой плотность молекул в точке, где U = 0.

Полученная формула, связывающая изменение плотности газа с потенциальной энергией его молекул, называется формулой Больцмана. Давление отличается от плотности постоянным множителем kT , поэтому такое же уравнение справедливо и для давления

В случае поля тяжести вблизи земной поверхности потенциальная энергия молекулы на высоте z равна U = mgz , где m – масса молекулы. Поэтому, если считать температуру газа не зависящей от высоты, то давление р на высоте z будет связано с давлением р 0 на поверхности Земли соотношением

Эту формулу называют барометрической формулой. Ее удобнее представить в виде

где m – молекулярный вес газа, R – газовая постоянная.

Эту формулу можно применять и в случае смеси газов. Поскольку молекулы идеальных газов практически не взаимодействуют друг с другом, каждый газ можно рассматривать отдельно, т. е. аналогичная формула применима к парциальному давлению каждого из них. Чем больше молекулярный вес газа, тем быстрее его давление убывает с высотой. Поэтому атмосфера по мере увеличения высоты все более обогащается легкими газами: кислород, например, убывает в атмосфере быстрее, чем азот.

Следует, однако, иметь в виду, что применимость барометрической формулы к реальной атмосфере весьма ограничена, поскольку атмосфера в действительности не находится в тепловом равновесии и ее температура меняется с высотой.

Из формулы Больцмана можно сделать интересное заключение, если попытаться применить ее к атмосфере на любых расстояниях от Земли. На очень больших расстояниях от земной поверхности под U нужно понимать не mgz , a точное значение потенциальной энергии частицы

где g – гравитационная постоянная, М – масса Земли и r – расстояние от центра Земли. Справедливость этого выражения легко проверить дифференцированием по расстоянию (F = - dU/dr) и последующим сравнением с законом всемирного тяготения. Подстановка этой энергии в формулу Больцмана дает следующее выражение для плотности газа:

где через n ¥ теперь обозначена плотность газа в месте, где U =0 (т. е. на бесконечном расстоянии от Земли). Если r равен радиусу Земли R , получится соотношение между плотностью атмосферы на поверхности Земли n 0 и на бесконечности n ¥ :

Согласно этой формуле плотность атмосферы на бесконечно большом расстоянии от Земли должна была бы быть отлична от нуля. Такой вывод, однако, абсурден, так как атмосфера имеет земное происхождение, и конечное количество газа не может быть распределено по бесконечному объему с нигде не исчезающей плотностью. Полученный вывод объясняется тем, что атмосфера предполагалась находящейся в состоянии теплового равновесия, что не соответствует действительности.

Данный результат показывает, что гравитационное поле вообще не может удержать газ в состоянии равновесия, а потому атмосфера должна непрерывно рассеиваться в пространстве. В случае Земли это рассеяние чрезвычайно медленно, и за все время своего существования Земля не потеряла сколько-нибудь заметной доли своей атмосферы. Но, например, в случае Луны с ее гораздо более слабым полем тяготения потеря атмосферы происходила гораздо быстрее, и в результате Луна в настоящее время атмосферы уже не имеет.

Некоторые представления о распределении молекул сразу же следуют из хаотичности теплового движения. Это относится к распределению молекул по направлениям скоростей или к распределению молекул по объему для случая, когда на газ не действуют какие-либо силы. Однако имеется множество случаев, для которых заранее не очевидны следствия допущения о хаотичности теплового движения.

Прежде всего, возникает вопрос о распределении молекул по величинам скоростей. Каков процент быстрых, средних по скорости, медленных молекул? Далее, может встать задача: найти, как изменится равномерное распределение молекул по плотностям при внесении газа в поле сил, скажем, в поле тяжести, или в электрическое или магнитное поле, если молекулы обладают электрическими или магнитными свойствами. На эти и подобные вопрось! отвечает закон

Больдмана, который можно вывести, используя аппарат теории вероятностей.

Рассмотрим небольшой объем пространства - кубик со сторонами построенный в точке Пусть в этом кубике находится значительное число молекул. Среди них мы отберем те, которые имеют компоненты скорости, лежащие в пределах от до от и от до Величины таковы, чтобы в указанном интервале скоростей находилось большое количество молекул. Это нужно для того, чтобы к этим малым объемам можно было применять законы статистической физики (физически бесконечно малые объемы). В дальнейшем будем говорить о таких молекулах, что они обладают координатами около и скоростями около Еще раз подчеркнем, что говорить о количестве молекул, обладающих точно заданной скоростью, нельзя, так как вероятность встретить такую молекулу бесконечно мала. Так как кинетическая энергия молекулы определяется значением скорости, а потенциальная энергия молекулы во внешнем поле зависит от координат молекулы в пространстве, то все выделенные нами молекулы имеют практически одну и ту же энергию

Закон Больцмана, обоснование которого следует искать в курсах теоретической физики, дает общее выражение для числа молекул, обладающих координатами около и скоростями около это число равно

здесь А - постоянная, которая может быть найдена для конкретной задачи, абсолютная температура постоянная Больцмана.

Энергия, входящая в экспоненту, является суммой кинетической энергии поступательного движения молекулы и ее потенциальной энергии во внешнем поле: Поэтому

Формула распространяется и на случай, когда молекула обладает и другими формами энергии, например вращательной или колебательной. Тогда эти составляющие энергии надо внести в

Закон Больцмана, или, как еще говорят, распределение Больцмана, показывает, что наибольшей энергии соответствует наименьшее число частиц, скорости и координаты которых лежат в заданном интервале.

Закон Больцмана мы применим для решения двух важных вопросов, касающихся распределения частиц с высотой и распределения молекул по скоростям.