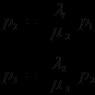Теоремы исследований уравнений и неравенств с параметром. Реферат: Решение уравнений, неравенств, систем с параметром (алгебра и начала анализа)
Класс: 11
Цели:
Образовательная:
- систематизировать и обобщить знания о решении уравнения с параметром;
- показать основные приемы решения таких уравнений.
Развивающая: расширить и углубить изучение различных приемов решения уравнений с параметром.
Воспитательная: показать значимость зависимости ответа в задаче с параметром от выбранного значения параметра.
Используемые методы обучения – их применение .
- Объяснительно-иллюстративный.
- Обобщения, аналогии и сравнения.
- УДЕ – создание ключевых задач, аналогия изображений на плоскости.
- Интегрированный – сопоставление алгебры и геометрические интерпретации, слайды.
Формирование общеучебных умений и навыков:
- Выделение существенных признаков изучаемых объектов;
- Выработка практических навыков;
- Используемые методы работы с аудиторией: работа в диалоговом режиме;
- Психологические аспекты урока;
- Создание комфортной рабочей атмосферы;
- Побуждение к активной диалоговой деятельности.
Ход урока
Введение . Вступительное слово учителя .
Уравнения стали привычной частью вариантов вступительных экзаменов ЕГЭ.
Уравнения с параметром вызывают серьезные трудности логического характера.
Каждое такое уравнение – это, по существу, краткая запись семейства уравнений. Ясно, что выписать каждое уравнение из бесконечного семейства невозможно, но тем не менее каждое из них должно быть решено. Поэтому возникает необходимость в рассмотрении системы понятий и поиске методов решения уравнений с параметрами (линейных, рациональных и т.д.)
Пусть дано уравнение F(х;а) = 0. Если придать параметру а какое – либо фиксированное значение, то данное уравнение можно рассматривать как «обычное» уравнение с одной переменной.
Поставим задачу : Выяснить, какой может быть ситуация при выбранном значении параметра?
Работа с учащимися в диалоговом режиме.
Обозначим основные проблемы:
- Установить основные понятия уравнений с параметрами.
- Для каждого вида уравнений школьного курса математики установить общий метод решения соответствующих уравнений с параметрами – единый как для одного, так и для двух параметров.
- Рассмотреть примеры заданий на исследование уравнений.
- Каково установление числа корней уравнений.
- Нахождение общего корня двух уравнений – в чем его суть?
- Геометрические интерпретации.
I этап – решение первой проблемы .
Работа с учащимися в диалоговом режиме .
Какие вопросы вы себе определите для установления основных понятий?
|
Появляется слайд и конспект
В задачах II типа требуется найти все значения параметра, при которых выполнены те или иные заданные условия. |
Например.
1) Решить уравнение а (а – 1) = а – 1.
Решение . Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а. Будем решать его «как обычно»: делим обе части уравнения на коэффициент при неизвестном. Но всегда ли возможно деление?
Делить на ноль нельзя. Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен о. Получим:
Ответ: 1) если а 0, а 1, то х = ;
2) если а = 1, то х – любое число;
3) если а = 0, то корней нет.
2) Решить уравнение (а – 1)х 2 + 2 (2а – 1)х + 4 а + 3 = 0.
Решение . Рассмотрим два случая:
Рассмотрим дискриминант: D = (2а – 1) 2 – (а – 1)(4а + 3) = - 3а + 4.
Если же а , то х 1,2 = ![]() .
.
Ответ: 1) если а > , то корней нет;
2) если а = 1, то х = - 3,5;
3) если а и а1, то х 1,2 = ![]() .
.
II этап – решение второй проблемы .
Рассмотрим способ классификации частных уравнений с помощью модели общих решений.
Появляется слайд.
Например. В рациональном уравнении  функция f 1 (а) = является общим решением для тех значений параметра, для которых
функция f 1 (а) = является общим решением для тех значений параметра, для которых ![]() . Поскольку
. Поскольку

общее решение уравнения на А f1 = }.
Функция f 2 (а) = есть общее решение уравнения на множестве А f2 = .
Построим модель общих решений в следующем виде

На модели выделяем все типы частных уравнений: ![]() ;
;  ;
;  .
.
Итак, на примерах рассмотрены основные понятия уравнений с параметрами: область допустимых значений; область определения; общие решения; контрольные значения параметров; типы частных уравнений.
На базе введенных параметров определим общую схему решения всякого уравнения F(а;х) = 0 с параметром а (для случая двух параметров схема аналогична):
- устанавливается область допустимых значений параметра и область определения;
- определяются контрольные значения параметра, разбивающие область допустимых значений параметра на области однотипности частных уравнений;
- для контрольных значений параметра соответствующие частные уравнения исследуются отдельно;
- находятся общие решения х = f 1 (а), …, f k (а) уравнения F(а;х) =0 на соответствующих множествах А f1 , ……, А fk значений параметра;
- составляется модель общих решений, контрольных значений параметра в следующем виде (на слайде);

- на модели выделяются промежутки значений параметра с одинаковыми решениями (области однотипности);
- для контрольных значений параметра и выделенных областей однотипности записываются характеристики всех типов частных решений.
III этап – примеры заданий на исследование уравнений.
Рассмотрим примеры решения задач с параметрами 2 типа.
Особенно часто встречаются задачи на расположение корней квадратного уравнения. При их решении хорошо «работают» графические иллюстрации. Расположение корней относительно заданных точек плоскостью определяется направлением ветвей соответствующей параболы, координатами вершины, а также значениями в заданных точках.
Например.
1) При каких значениях параметра а уравнение (а 2 + а + 1)х 2 + (2а – 3)х + а – 5 = 0 имеет два корня, один из которых больше 1, а другой меньше 1?
Решение . Пусть f(х) = (а 2 + а + 1)х 2 + (2а – 3)х + а – 5. Так как а 2 + а + 1 >0, то для квадратичной функции f(х) условие задачи может выполняться только при условии f (х) < 1.

Решая неравенство f(1) = а 2 + 4а – 7 < 0, получим, что -2 - < а < - 2 + .
Ответ : -2 - < а < - 2 + .
2) При каких значениях параметра m корни уравнения (m – 1)х 2 – 2 mх + m + 3 = 0 положительны?
Решение . Пусть f(х) = (m-1)х 2 - 2 mх + m + 3 тогда:
1) если, m = 1,то -2х + 4=0, х= 2- корень положителен;
2) если m 1, то с помощью рисунка можно получить следующие соотношения:


Рассмотрим 2 случая:
1) если 1,5 m > 0, тогда из 2 и 3 неравенств последней системы получим, что m > 1, т.е. окончательно 1,5 m > 1;
2) если m < 0, тогда из неравенства (m-1)m > 0 получим, что m-1 < 0, откуда m + 3 < 0, т.е. окончательно m < -3.
Ответ : m (-; -3)
IV этап - рассмотрим задачи на установления числа корней уравнения.
Пример 1. При каких значениях параметра, а уравнение 2 cos 2 x – (2а + 9)cosx + 9а = 0 не имеет корней.
Решение. Пусть у = cosх, тогда исходное уравнение примет вид 2у 2 – (2 а + 9)у + 9а = 0, корни которого у 1 = а, у 2 = 4,5. Уравнение cosх = 4,5 корней не имеет, а уравнение cosх = а не имеет корней, если > 1.
Ответ : (- ; -1) (1; ).
Пример 2
.
Найдите все значения параметра а, при которых уравнение ![]() не имеет корней.
не имеет корней.
Решение
. Данное уравнение равносильно системе: 
![]() .
.
Уравнение не имеет решения в двух случаях: а = и
Пример 3
. При каких значениях параметра а уравнение ![]() имеет единственное решение?
имеет единственное решение?
Решение . Решение уравнения может быть единственным только, если х = 0. Если х = 0,то а 2 -1 = 0, и а = 1.
Рассмотрим 2 случая:
1) если а = 1, то х 2 - = 0 – корней три;
2). Если а = -1, то то х 2 + = 0, х = 0 - единственный корень.
Пример 4. При каких значениях параметра а уравнение имеет 2 корня?
Решение. Данное уравнение равносильно системе: . Выясним, когда квадратное уравнение х 2 – х – а = 0 имеет 2 неотрицательных корня.
Полученное уравнение имеет два корня, если 1+ 4а > 0; они неотрицательны, если
 0 > а > - .
0 > а > - .
Ответ : (- ; 0] .
Во многих случаях при установлении числа корней уравнении имеет значение симметрия.
V этап - нахождение общего корня двух уравнений.
Пример 1. При каких значениях параметра а уравнение х 2 + 3х + 7а -21 =0 и х 2 +6х +5а -6 =0 имеют общий корень?
Решение. Исключим параметр а из полученной системы. Для этого первое уравнение умножим на -5, второе - на7, а результаты сложим. Получим: 2х 2 + 27х +63 =0, корни которого х 1 = -3, х 2 = -10,5. Подставим корни в одно из уравнений и найдем значение параметра а.
Ответ : 3 и – 8,25.
Пример 2. При каких значениях параметра а уравнение х 2 – ах + 2 = 0 и 3х 2 + (а - 9)х+ 3=0 равносильны?
Решение . Как известно уравнения равносильны, если множество их корней совпадают. Рассмотрим 2 случая.
1) Уравнения не имеют корней (множество корней пусто). Тогда их дискриминанты отрицательны:


Система неравенств решений не имеет.
2) Уравнения имеют общие корни. Тогда 



Следовательно, данные уравнения могут иметь общие корни только при а = 3 или а = .
Проверить самостоятельно!
VI этап – геометрические интерпретации.
Решение задач с параметрами может существенно облегчить использование графиков.
Пример 1
. Решите уравнение в зависимости от параметра а: ![]() .
.
Решение. Понятно что при а 0:
Все ли корни подходят. Чтобы это выяснить, построим график функции а =.
Количество корней можно увидеть на рисунке:

- если а < 0, то корней нет;
- если а = 0 и а > 0, то 2 корня.
Найдем эти корни.
При а = 0 получим х 2 – 2х – 3 = 0 и х 1 = -1, х 2 = 3; при а > 4 это корни уравнения х 2 – 2х – 3 – а = 0.
Если 0 < а < 4 – все 4 корня подходят.
Если а = 4 – три корня:
Ответ
: 1) если а < 0, то корней нет;
2) если а = 0, то х 1 = -1, х 2 =3;
3) если 0 < a < 4, то х 1,2,3.4 = 1 ;
4) если а = 4, то х 1 = 1; х 2,3 = 1 ;
5) если а > 4, то х 1,2 = 1 .
Пример 2 . При каких значениях а уравнение имеет более двух корней?
Решение . Если подставить х = 0 в исходное уравнение, то получим 6 = 6, это означает, что х = 0 является решением уравнения при любом а.
Пусть теперь х 0, тогда можно записать ![]() . Выясним знаки выражений 2х + 3 и 2х – 3.
. Выясним знаки выражений 2х + 3 и 2х – 3.

Раскроем модули: а =  (1)
(1)
В плоскости х0а построим множество точек (х;а), координаты которых удовлетворяют соотношению (1).

Если а = 0, то уравнение имеет бесконечное множество решений на промежутке , при других значениях а число решений уравнения не превышает двух.
Ответ : а = 0.
Тестовый контроль
1 вариант |
2 вариант |
1) Решите уравнение: 0 · х = а Ответы |
1) Решить уравнение: а х = а. Ответы : а) при а ≠ 0, х = 1, при а = 0, х R б) при а = 0, х R, при а ≠ 0 корней нет в) при а = 0 нет корней, при а ≠ х = |
2) Решит уравнение: (в – 2)·х = 5 + в. Ответы: |
2) Решите уравнение (в + 1)·х = 3 – в . Ответы: а) при в = 2 нет корней; при в ≠2, х = ; б) при в = -2 нет корней, при в ≠-2 х = в) при в = -1 нет корней, при а ≠ - 1 |
3) При каких значениях параметра с уравнение имеет бесконечное множество решений? с·(с + 1)·х = с 2 – 1 . Ответ : а) при с = -1, х R, ; |
Параметр \(a\)
– это число, которое может принимать любые значения из \(\mathbb{R}\)
.
Исследовать уравнение/неравенство при всех значениях параметра – это значит указать, при каких значениях параметра какое именно решение имеет данное уравнение/неравенство.
Примеры:
1) уравнение \(ax=2\)
при всех \(a\ne 0\)
имеет единственное решение \(x=\dfrac 2a\)
, а при \(a=0\)
не имеет решений (т.к. тогда уравнение принимает вид \(0=2\)
).
2) уравнение \(ax=0\)
при всех \(a\ne 0\)
имеет единственное решение \(x=0\)
, а при \(a=0\)
имеет бесконечно много решений, т.е. \(x\in
\mathbb{R}\)
(т.к. тогда уравнение принимает вид \(0=0\)
).
Заметим, что
I) обе части уравнения нельзя делить на выражение, содержащее параметр (\(f(a)\)
), если это выражение может быть равно нулю. Но можно рассмотреть два случая:
первый, когда \(f(a)\ne0\)
, и в этом случае можно разделить обе части равенства на \(f(a)\)
;
второй случай, когда \(f(a)=0\)
, и этом случае мы можем по отдельности проверить каждое значение \(a\)
(см. пример 1, 2).
II) обе части неравенства нельзя делить на выражение, содержащее параметр, если неизвестен знак этого выражения. Но можно рассмотреть три случая:
первый, когда \(f(a)>0\)
, и в этом случае можно делить обе части неравенства на \(f(a)\)
;
второй, когда \(f(a)<0\)
, и в этом случае при делении обеих частей неравенства на \(f(a)\)
мы обязаны поменять знак неравенства на противоположный;
третий, когда \(f(a)=0\)
, и в этом случае мы можем по отдельности проверить каждое значение \(a\)
.
Пример:
3) неравенство \(ax>3\) при \(a>0\) имеет решение \(x>\dfrac3a\) , при \(a<0\) имеет решение \(x<\dfrac3a\) , а при \(a=0\) не имеет решений, т.к. принимает вид \(0>3\) .
Задание 1 #1220
Уровень задания: Легче ЕГЭ
Решите уравнение \(ax+3=0\)
Уравнение можно переписать в виде \(ax=-3\) . Рассмотрим два случая:
1) \(a=0\) . В этом случае левая часть равна \(0\) , а правая – нет, следовательно, уравнение не имеет корней.
2) \(a\ne 0\) . Тогда \(x=-\dfrac{3}{a}\) .
Ответ:
\(a=0 \Rightarrow x\in \varnothing; \\ a\ne 0 \Rightarrow x=-\dfrac{3}{a}\) .
Задание 2 #1221
Уровень задания: Легче ЕГЭ
Решите уравнение \(ax+a^2=0\) при всех значениях параметра \(a\) .
Уравнение можно переписать в виде \(ax=-a^2\) . Рассмотрим два случая:
1) \(a=0\) . В этом случае левая и правая части равны \(0\) , следовательно, уравнение верно при любых значениях переменной \(x\) .
2) \(a\ne 0\) . Тогда \(x=-a\) .
Ответ:
\(a=0 \Rightarrow x\in \mathbb{R}; \\ a\ne 0 \Rightarrow x=-a\) .
Задание 3 #1222
Уровень задания: Легче ЕГЭ
Решите неравенство \(2ax+5\cos\dfrac{\pi}{3}\geqslant 0\) при всех значениях параметра \(a\) .
Неравенство можно переписать в виде \(ax\geqslant -\dfrac{5}{4}\) . Рассмотрим три случая:
1) \(a=0\) . Тогда неравенство принимает вид \(0\geqslant -\dfrac{5}{4}\) , что верно при любых значениях переменной \(x\) .
2) \(a>0\) . Тогда при делении на \(a\) обеих частей неравенства знак неравенства не изменится, следовательно, \(x\geqslant -\dfrac{5}{4a}\) .
3) \(a<0\) . Тогда при делении на \(a\) обеих частей неравенства знак неравенства изменится, следовательно, \(x\leqslant -\dfrac{5}{4a}\) .
Ответ:
\(a=0 \Rightarrow x\in \mathbb{R}; \\ a>0 \Rightarrow x\geqslant -\dfrac{5}{4a}; \\ a<0 \Rightarrow x\leqslant -\dfrac{5}{4a}\) .
Задание 4 #1223
Уровень задания: Легче ЕГЭ
Решите неравенство \(a(x^2-6) \geqslant (2-3a^2)x\) при всех значениях параметра \(a\) .
Преобразуем неравенство к виду: \(ax^2+(3a^2-2)x-6a \geqslant 0\) . Рассмотрим два случая:
1) \(a=0\) . В этом случае неравенство становится линейным и принимает вид: \(-2x \geqslant 0 \Rightarrow x\leqslant 0\) .
2) \(a\ne 0\) . Тогда неравенство является квадратичным. Найдем дискриминант:
\(D=9a^4-12a^2+4+24a^2=(3a^2+2)^2\) .
Т.к. \(a^2 \geqslant 0 \Rightarrow D>0\) при любых значениях параметра.
Следовательно, уравнение \(ax^2+(3a^2-2)x-6a = 0\) всегда имеет два корня \(x_1=-3a, x_2=\dfrac{2}{a}\) . Таким образом, неравенство примет вид:
\[(ax-2)(x+3a) \geqslant 0\]
Если \(a>0\)
, то \(x_1
Если \(a<0\) , то \(x_1>x_2\) и ветви параболы \(y=(ax-2)(x+3a)\) направлены вниз, значит, решением являются \(x\in \big[\dfrac{2}{a}; -3a]\) .
Ответ:
\(a=0 \Rightarrow x\leqslant 0; \\ a>0 \Rightarrow x\in (-\infty; -3a]\cup \big[\dfrac{2}{a}; +\infty); \\ a<0 \Rightarrow x\in \big[\dfrac{2}{a}; -3a\big]\) .
Задание 5 #1851
Уровень задания: Легче ЕГЭ
При каких \(a\) множество решений неравенства \((a^2-3a+2)x -a+2\geqslant 0\) содержит полуинтервал \(\) .
Ответ:
\(a\in (-\infty;\dfrac{4}{3}\big]\cup
Рассмотрим два случая:
1) \(a+1=0 \Rightarrow a=-1\) . В этом случае уравнение \((*)\) равносильно \(3=0\) , то есть не имеет решений.
Тогда вся система равносильна \(\begin{cases} x\geqslant 2\\ x=2 \end{cases} \Leftrightarrow x=2\)
2) \(a+1\ne 0 \Rightarrow a\ne -1\) . В этом случае система равносильна: \[\begin{cases} x\geqslant -2a\\ \left[ \begin{gathered} \begin{aligned} &x_1=-2a \\ &x_2=\dfrac3{a+1} \end{aligned} \end{gathered} \right. \end{cases}\]
Данная система будет иметь одно решение, если \(x_2\leqslant -2a\) , и два решения, если \(x_2>-2a\) :
2.1) \(\dfrac3{a+1}\leqslant -2a \Rightarrow a<-1 \Rightarrow \) имеем один корень \(x=-2a\) .
2.2) \(\dfrac3{a+1}>-2a \Rightarrow a>-1 \Rightarrow \) имеем два корня \(x_1=-2a, x_2=\dfrac3{a+1}\) .
Ответ:
\(a\in(-\infty;-1) \Rightarrow x=-2a\\ a=-1 \Rightarrow x=2\\ a\in(-1;+\infty) \Rightarrow x\in\{-2a;\frac3{a+1}\}\)
Как показывает статистика, нахождение решения задач с параметром многие выпускники считают наиболее трудным при подготовке в ЕГЭ 2019 по математике. С чем это связано? Дело в том, что зачастую задачи с параметром требуют применения исследовательских методов решения, т. е. при вычислении правильного ответа понадобится не просто применять формулы, но и находить те параметрические значения, при которых выполнено определенное условие для корней. При этом сами корни порой искать вовсе не требуется.
Тем не менее справляться с решением заданий с параметрами должны все учащиеся, которые готовятся к сдаче ЕГЭ. Подобные задачи встречаются в аттестационном испытании регулярно. Образовательный портал «Школково» поможет вам восполнить пробелы в знаниях и научиться быстро находить решение заданий с параметром в ЕГЭ по математике. Наши специалисты подготовили и в доступной форме изложили весь базовый теоретический и практический материал по данной теме. С порталом «Школково» решение задач на подбор параметра будет даваться вам легко и не повлечет никаких затруднений.
Основные моменты
Важно понять, что единого алгоритма решения задач на подбор параметра попросту не существует. Способы нахождения правильного ответа могут быть различными. Решить математическую задачу с параметром в ЕГЭ - значит, найти, чему равна переменная при определенном значении параметра. Если исходное уравнение и неравенство можно упростить, это необходимо сделать в первую очередь. В некоторых задачах для этого можно использовать стандартные методы решения, как в случае, если бы параметр представлял собой обычное число.
Вы уже успели ознакомиться с теоретическим материалом по данной теме? Для окончательного усвоения информации при подготовке к ЕГЭ по математике рекомендуем попрактиковаться в выполнении заданий с параметром; для каждого упражнения мы представили полный разбор решения и правильный ответ. В соответствующем разделе вы найдете как простые, так и более сложные задачи. Попрактиковаться в решении упражнений с параметрами, построенных по примеру заданий в ЕГЭ, учащиеся могут в режиме онлайн, находясь в Москве или любом другом городе России.
Урок по элективному курсу
по теме: «Решение уравнений и неравенств с параметрами»
(Урок обобщения и повторения)
Цель: 1.Повторить и обобщить знания учащихся методов решения уравнений и неравенств с параметрами; закрепить умения применять знания при решении конкретных заданий; 2. Развивать логическое мышление; 3.Воспитывать внимание и аккуратность.
План урок: I. Организационный момент_________________________2 мин.
II. Актуализация опорных знаний:
- Повторение__________________________________3 мин.
- Устная работа________________________________3 мин.
- Работа по карточкам (во время 1 и 2)
III. Решение упражнений___________________________22 мин.
IY. Выполнение теста______________________________8 мин.
Y. Подведение итогов, постановка домашнего задания__2 мин.
Х о д у р о к а:
I. Организационный момент .
Учитель: - Здравствуйте, ребята. Приятно вас всех видеть, мы начинаем наш урок. Сегодня на уроке наша цель - повторить и отработать знания, умения и навыки, полученные на прошлых уроках при изучении данной темы.
II . Актуализация опорных знаний:
1) Повторение.
Учитель: - Итак, повторим.
Что называется линейным уравнением с параметрами?
Какие случаи мы рассматривали при решении таких уравнений?
Приведите примеры линейных уравнений с параметрами.
Приведите примеры линейных неравенств с параметрами.
2) Устная работа.
Задание: Приведите данное уравнение к линейному виду.
На доске:
а) 3а х – 1 =2 х ;
б) 2+5 х = 5а х ;
в) 2 х – 4 = а х + 1.
3) Работа по карточкам.
III . Решение упражнений.
Задание 1. Решить уравнение с параметром а.
3(ах + 1) + 1 = 2(а – х) + 1.
Задание выполняется на доске и в тетрадях.
Задание 2. При каком значении а, прямая у = 7ах + 9, проходит через
т. А(-3;2) ?
Задание выполняется самостоятельно у доски одним учеником. Остальные работают в тетрадях, затем сверяются с доской.
Физкульт. минутка.
Задание 3. При каком значении а, уравнение 3(ах – а) = х – 1 имеет
Бесконечно много решений?
Данное задание предлагается решить самостоятельно учащимся в тетрадях. Затем проверить ответы.
Задание 4. При каком значении параметра а , сумма корней уравнения
2х² + (4а² - 2)х – (а² + 1) = 0 равна 1?
Задание выполняется комментированием с места.
Задание 5. Решите неравенство с параметром р :
р(5х – 2)
Данное задание выполняется у доски и в тетрадях.
IY. Выполнение теста.
Учащимся выдаются индивидуальные листы с заданиями:
1) Является ли уравнение 6(ах + 1) + а = 3(а – х) + 7 линейным?
А) да; б) нет; в) можно привести к линейному
2) Уравнение (2ах + 1)а = 5а – 1 приведено к виду линейного уравнения
А) нет; б) да;
3) При каком значении параметра а прямая у = ах – 3 проходит через
Т. А(-2;9) ?
А) а = 1/6; б) а = 1/2; в) а = -6; г) а = 6.
4) При каком а уравнение 2ах + 1 = х имеет корень, равный -1?
а) а = -1; б) а = 0; в) а = 1; г) а = 1/2.
5) Если у квадратного уравнения ах² + вх + с = 0 Д ах² + вх + с >0 зависит от
А) значения в ; б) значения а ; в) значения -в/а ;
г) не имеет решений.
О т в е т ы к т е с т у: в; а; в; в; б.
YII. Подведение итогов урока. Постановка домашнего задания.
Учитель: - Сегодня на уроке мы повторили и закрепили знания, полученные на прошлых уроках, отработали необходимые умения при выполнении различных заданий. Я думаю, что вы поработали хорошо, молодцы.
Кроме поставленных за урок оценок, можно оценить работу на уроке еще ряда учащихся.
Учитель : - Запишите домашнее задание:
На доске:
Решить неравенство: х² - 2ах + 4 > 0.
Урок окончен.
Человек, умеющий решать задачи с параметрами, в совершенстве знает теорию и умеет ее применять не механически, а с логикой. Он «понимает» функцию, «чувствует» ее, считает ее своим другом или хотя бы хорошим знакомым, а не просто знает о ее существовании.
Что же такое уравнение с параметром? Пусть дано уравнение f (x; a) = 0. Если ставится задача отыскать все такие пары (x; a), которые удовлетворяют данному уравнению, то оно рассматривается как уравнение с двумя равноправными переменными х и а. Но можно поставить и другую задачу, полагая переменные неравноправными. Дело в том, что если придать переменной а какое-либо фиксированное значение, то f (x; a) = 0 превращается в уравнение с одной переменной х, и решения этого уравнения, естественно, зависят от выбранного значения а.

Основная трудность, связанная с решением уравнений (и тем более неравенств) с параметром, состоит в следующем: -при одних значениях параметра уравнение не имеет решений; -при других – имеет бесконечно много решений; -при третьих – оно решается по одним формулам; - при четвертых – оно решается по другим формулам. - Если уравнение f (x; a) = 0 нужно решить относительно переменной Х, а под a понимается произвольное действи- тельное число, то уравнение называют уравнением с параметром a.

Решить уравнение с параметром f (x; a) = 0 – это решить семейство уравнений, получающихся из уравнения f (x; a) = 0 при любых действительных значениях параметра. Уравнение с параметром – это, по сути дела, краткая запись бесконечного семейства урав- нений. Каждое из уравнений семейства полу- чается из данного уравнения с параметром при конкретном значении параметра. Поэтому задачу решения уравнения с параметром можно сформулировать следующим образом:

Выписать каждое уравнение из бесконечного семейства уравнений невозможно, но тем не менее каждое уравнение из бесконечного семейства должно быть решено. Сделать это, например, можно, если по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества, а затем заданное уравнение решить на каждом из этих подмножеств. Решение линейных уравнений

Чтобы разбить множество значений параметра на подмножества, полезно воспользоваться теми значениями параметра, при которых или при переходе через которые происходит качественное изменение уравнения. Такие значения параметра можно назвать контрольными или особыми. Искусство решения уравнения с параметрами как раз и состоит в том, чтобы уметь находить контрольные значения параметра.


Тип 1. Уравнения, неравенства, их системы, которые необходимо решить либо для любого значения параметра, либо для значений параметра, принадлежащих заранее оговоренному множеству. Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.

Тип 2. Уравнения, неравенства, их системы, для которых требуется определить количество решений в зависимости от значения параметра (параметров). При решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы, ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Но иногда прямое решение является единственным разумным путем получения ответа при решении задачи типа 2.

Тип 3. Уравнения, неравенства, их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений). Задачи типа 3 в каком-то смысле обратны задачам типа 2.

Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения. Например, найти значения параметра, при которых: 1) уравнение выполняется для любого значения переменной из заданного промежутка; 2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.

Основные способы (методы) решения задач с параметром. Способ I (аналитический). Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им. Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости Оху, или в координатной плоскости Оха. Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.

Пример 1. Найти значения параметра а, при которых уравнение а(2а + 3)х + а 2 = а 2 х + 3а имеет единственный отрицательный корень. Решение. Данное уравнение равносильно следующему:. Если а(а + 3) 0, то есть а 0, а –3, то уравнение имеет единственный корень х =. х

Пример 2. Решите уравнение. Решение. Так как знаменатель дроби не может равняться нулю, имеем (b – 1)(x + 3) 0, то есть b 1, x –3. Умножив обе части уравнения на (b – 1)(x + 3) 0, получаем уравнение: Это уравнение является линейным относительно переменной х. При 4b – 9 = 0, то есть b = 2,25 уравнение принимает вид: При 4b – 9 0, то есть b 2,25 корень уравнения x =. Теперь надо проверить, нет ли таких значений b, при которых найденное значение х равно –3. Таким образом, при b 1, b 2,25, b –0,4 уравнение имеет единственный корень x =. О т в е т: при b 1, b 2,25, b –0,4 корень x = при b = 2,25, b = –0,4 решений нет; при b = 1 уравнение не имеет смысла.

Типы задач 2 и 3 отличает то, что при их решении не требуется получить явное решение, а нужно лишь найти те значения параметра, при которых это решение удовлетворяет тем или иным условиям. Примерами таких условий для решения могут служить следующие: существует решение; не существует решения; существует единственное решение; существует положительное решение; существует ровно k решений; существует решение, принадлежащее указанному промежутку. В этих случаях оказывается очень полезен графический способ решения задач с параметрами.

Можно выделить две разновидности применения графического метода при решении уравнения f (х) = f (а): На плоскости Оху рассматриваются график у = f (х) и семейство графиков у = f (а). Сюда же относятся задачи, решаемые с помощью «пучка прямых». Этот способ оказывается удобен в задачах с двумя неизвестными и одним параметром. На плоскости Оха (которую называют также фазовой) рассматриваются графики, в которых х – аргумент, а а – значение функции. Этот способ обычно применяется в задачах, в которых фигурируют лишь одна неизвестная и один параметр (или сводящиеся к таким).

Пример 1. При каких значениях параметра а уравнение 3х 4 + 4х 3 – 12х 2 = а имеет не менее трех корней? Решение. Построим графики функций f (х) = 3х 4 + 4х 3 – 12х 2 и f (х) = а в одной системе координат. Имеем: f "(х) = 12х х 2 – 24х = 12х(х + 2)(х – 1), f "(х) = 0 при х = –2 (точка минимума), при х = 0 (точка максимума) и при х = 1 (точка максимума). Найдем значения функции в точках экстремума: f (–2) = –32, f (0) = 0, f (1) = –5. Строим схематически график функции с учетом точек экстремума. Графическая модель позволяет ответить на поставленный вопрос: уравнение 3х 4 + 4х 3 – 12х 2 = а имеет не менее трех корней, если –5

Пример 2. Сколько корней при различных значениях параметра а имеет уравнение? Решение. Ответ на поставленный вопрос связан с числом точек пересечения графика полуокружности у = и прямой у = х + а. Прямая, являющаяся касательной, имеет формулу у = х +. Заданное уравнение не имеет корней при а; имеет один корень при –2

Пример3. Сколько решений имеет уравнение |х + 2| = ах + 1 в зависимости от параметра а? Решение. Можно построить графики у = |х + 2| и у = ах + 1. Но мы поступим иначе. При х = 0 (21) решений нет. Разделим уравнение на х: и рассмотрим два случая:1)х > –2 или х=2 2)2) х
–2 или х=2 2)2) х

Пример использования «пучка прямых» на плоскости. Найдите значения параметра a, при которых уравнение |3x + 3| = ax + 5 имеет единственное решение. Решение. Уравнение |3x + 3| = ax + 5 равносильно следующей системе: Уравнение y – 5 = a(x – 0) задает на плоскости пучок прямых с центром A (0; 5). Проведем прямые из пучка прямых, которые будут параллельны сторонам уголка, являющегося графиком y = |3x + 3|. Эти прямые l и l 1 пересекают в одной точке график y = |3x + 3|. Уравнения этих прямых y = 3x + 5 и у = –3х + 5. Кроме того, всякая прямая из пучка, расположенная между этими прямыми, также будет пересекать график y = |3x + 3| в одной точке. Значит, искомые значения параметра [–3; 3].

Алгоритм решения уравнений с использованием фазовой плоскости: 1. Находим область определения уравнения. 2. Выражаем параметр а как функцию от х. 3. В системе координат хОа строим график функции а = f(х) для тех значений х, которые входят в область определения данного уравнения. 4. Находим точки пересечения прямой а = с, где с є (-; +) с графиком функции а = f(х). Если прямая а = с пересекает график а = f(х), то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение а = f(х) относительно х. 5.Записываем ответ.

Пример решения неравенства с помощью «фазовой плоскости». Решите неравенство х. Решение.По равносильному переходу Теперь на плоскости Оха построим графики функций Точки пересечения параболы и прямой х 2 – 2х = –2х х = 0. Условие а –2х автоматически выполняется при а х 2 – 2х Таким образом, в левой полуплоскости (х

ФБГОУ ВПО «Мордовский государственный
педагогический институт имени М.Е. евсевьева»
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра математики и методики обучения математики
КУРСОВАЯ РАБОТА
Методика формирования умений решать уравнения и неравенства с параметрами в курсе основной общеобразовательной школе
студентка группы МДМ-110 А.И. Зимина
Специальность: 050201.65 «Математика» с дополнительной специальностью 050202 «Информатика»
Саранск 2014
Введение
Теоретические основы линий уравнений и неравенств в школьном курсе математики
1 Виды уравнений в школьном курсе математики
2 Виды неравенств в школьном курсе математики
3 Особенности решения уравнений с параметрами
4 Особенности решения неравенств с параметрами
Заключение
Список используемой литературы
Введение
На современном этапе развития школьного образования становятся приоритетными развивающие цели обучения. В связи с этим при изучении математики особую значимость приобретает организованное обучение приемам мышления, рационального выполнения учебной деятельности, что исключительно важно при усвоении трудных тем и решении сложных задач таких, как уравнения и неравенства с параметрами. Именно недостаточная сформированность приемов учебной деятельности является одной из причин того, что большинство учащихся совершает ошибки или испытывает затруднения при решении даже несложных задач такого рода.
Изучением задач с параметрами, их роли в обучении, понятий, связанных с их решением, в разные годы занимались М.И. Башмаков, Г.В. Дорофеев, М.И. Зайкин, Т.А. Иванова, Г.Л. Луканкин, Я.Л. Крейнин, В.К. Марков, А.Г. Мордкович, Н.Х. Розов, Г.И. Саранцев, Р.А. Утеева и др. Многие из них подчеркивали важность обучения школьников приемам решения уравнений и неравенств с параметрами прежде всего в связи с необходимостью подготовки учащихся к выполнению работ итоговой аттестации и различного рода конкурсных испытаний. При этом большинство авторов характеризует задачи с параметрами как исследовательские задачи, требующие высокой логической культуры и техники исследования; как наиболее сложные в логическом и семантическом плане вопросы элементарной математики. В этой связи В.В. Вересова, В.И. Горбачев, Н.С. Денисова, В.Н. Литвиненко, А.Г. Мордкович, Т.Н. Полякова, Г.А. Ястребинецкий и др. справедливо замечают, что для описания процесса их решения необходимо использовать систему понятий, математических утверждений и фактов, определяемую фундаментальными математическими идеями; некоторые из них предпринимают попытки к ее разработке. Однако в многочисленных пособиях и руководствах справочного и методического характера для поступающих в вузы рассматриваются лишь частные приемы решения конкретных уравнений и неравенств с параметрами, чаще всего в рамках широкого спектра конкурсных заданий.
Уравнения и неравенства, содержащие параметр, не изучаются систематически в школьном курсе математики, а рассматриваются лишь отдельные их простейшие примеры. Поэтому методы и приемы решения таких задач большинству учащихся не известны.
Актуальность данной темы состоит в том, что анализируя экзаменационные работы по математике, приходишь к выводу, что за курс математики в общеобразовательной школе учащимися должны быть отработаны умения решения задач с параметрами. Кроме непосредственной подготовки учащихся к экзаменам по данному разделу математики (решение задач с параметрами), главная его задача - поднять на более высокий уровень изучение математики в школе, следующий за развитием умений и навыков решения определенного набора стандартных задач.
Объект исследования: процесс формирования умений решать уравнений и неравенств с параметрами в школьном курсе метематике основной школы.
Предмет исследования: уравнения и неравенства с параметрами.
Цель исследования: выделить виды, методы решения уравнений и неравенств с параметрами в школьном курсе математике.
Для достижения поставленной цели необходимо было решить следующие задачи:
) Изучить и проанализировать специальную литературу по проблеме исследования;
)Рассмотреть роль уравнений и неравенств в школьном курсе математике;
1. Теоретические основы линий уравнений и неравенств в школьном курсе математики
Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно-методическую линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой, функциональной и другими линиями школьного курса математики.
Выделенным областям возникновения и функционирования понятия уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.
а) Прикладная направленность линии уравнений и неравенств раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.
В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.
б) Теоретико-математическая направленность линии уравнений и неравенств раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, неравенств и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений и неравенств связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений и неравенств.
в) Для линии уравнений и неравенств характерна направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией. Основная идея, реализуемая в процессе установления взаимосвязи этих линий, - это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений, неравенств, систем. Например, числовые промежутки выделяются неравенствами или системами неравенств. Области иррациональных и логарифмических выражений связаны соответственно с уравнениями (k-натуральное число, большее 1.
Связь линии уравнений и неравенств с числовой линией двусторонняя. Приведенные примеры показывают влияние уравнений и неравенств на развертывание числовой системы. Обратное влияние проявляется в том, что каждая вновь введенная числовая область расширяет возможности составления и решения различных уравнений и неравенств.
Линия уравнений и неравенств тесно связана также и с функциональной линией. Одна из важнейших таких связей приложения методов, разрабатываемых в линии уравнений и неравенств, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т.д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем.
1 Виды уравнений в школьном курсе математике
Понятие «уравнение » относится к важнейшим общематематическим понятиям.
Существуют различные трактовки понятия «уравнение».
И.Я. Виленкин и др. приводит логико - математическое определение уравнения. Пусть на множестве М зафиксирован набор алгебраических операций, х - переменная на М; тогда уравнением на множестве М относительно x называется предикат вида, где и - термы относительно заданных операций, в запись которого входит символ.Аналогично определиться уравнение от двух и более переменных.
Принятые в логики термины «терм» и «предикат» соответствуют такие термины школьной математики как «выражение» и «предложение с переменной». Поэтому наиболее близко к приведенному формальному определению можно считать следующее определение: «Предложение с переменной, имеющий вид равенства между двумя выражениями с этой переменной, называется уравнением». Такое определение приведено в учебнике «Алгебра и начала анализа» А.Н Колмогоров и др. Равенство с переменной называется уравнением. Значение переменной при котором равенство с переменной обращается в верное числовое равенство, называется корнем уравнения.
Часто, особенно в начале систематического курса алгебры, понятие уравнение вводится по средством выделение его из алгебраического метода решения задач. Например, в учебнике Ш.А.Алимова и др. понятие уравнение вводиться на материале текстовой задачи. Переход к понятию уравнения осуществляется на основе анализа некоторых формальных особенностей записи, выражающих содержание данной задачи в алгебраической форме: «Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением». Указываемый способ введения понятия уравнения соответствует еще одному компоненту понятия уравнения - прикладному.
Еще один подход к понятию уравнения получается при составления области определения уравнения и множества его корней. Например, в учебнике Д.К.Фадеева «Буквенное равенство, которое не обязательно превращается в верное числовое равенство при допустимых наборов букв, называется уравнение».
Можно встретить и третий вариант определения, роль которого проявляется при изучения графического метода решения уравнений: «Уравнение - это равенство двух функций».
Среди всех изучаемых в курсе математике типов уравнений В.И. Мишин выделяет сравнительно ограничение количество основных типов. к их числу относится: линейное уравнение с одним неизвестным, систему двух линейных уравнений с двумя неизвестными, квадратные уравнения, простейшие иррациональные и трансцендентные.
Ю.М.Колягин и др. классифицируют по виду функций, представляющих правую и левую части уравнений:
Уравнение называется:
алгебраическим, если и - алгебраические функции;
трансцендентным, если хотя одним из функций и трансцендентная;
рациональным алгебраическим (или просто рациональным) , если алгебраические функции и рациональные;
иррациональным алгебраическим(или просто иррациональным), если хотя бы одна из алгебраических функций и иррациональная;
целым рациональным, если функция и целые рациональные;
дробным рациональным, если хотя бы одна из рациональных функций и дробная рациональная.
Уравнение, где - многочлен стандартного вида, называется линейным (первой степени), квадратным(во второй степени), кубическим (третьей степени) и вообще - ой степени, если многочлен, имеет соответственно первую, вторую, третью и вообще - ую степень.
В школе изучаются несколько типов уравнений. К их числу относятся: линейные уравнения с одной не известной, квадратные уравнения, иррациональные и трансцендентные уравнения, рациональные уравнения. Эти типы уравнений изучаются с большой тщательностью, для них указывается и доводиться до автоматизма выполнение алгоритма решения, указывается форма, в котором должен записываться ответ.
Виды уравнений и методы решения:
) Линейное уравнение
Уравнением с одной переменной, называется равенство, содержащее только одну переменную.
Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.
Найти все корни уравнения или доказать, что их нет - это значит решить уравнение.
Пример 1: Решить уравнение.
;
;
) Квадратное уравнение
Квадратное уравнение - это уравнение вида, где коэффициенты a, b и c - любые действительные числа, причем а≠0.
Корнями квадратного уравнения называют такие значения переменной, при которых квадратное уравнение обращается в верное числовое равенство.
Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.
Пример 2: Решить уравнение
Данное уравнение можно решить либо через Теорему Виета, либо через дискриминант.
Ответ: х1=-1, х2=-2.
) Рациональные уравнения
рациональные уравнения - уравнения вида
где и многочлены, атак же уравнения вида, где и - рациональные.
Пример 3: Решить уравнение
) Иррациональные уравнения
Иррациональные уравнения - это уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Пример 4: Решить уравнение
Возведем обе части в квадрат:
) Показательные и логарифмические уравнения
При решения показательных уравнений используются два основных метода: а) переход от уравнения к уравнению;б) введения новых переменных. Иногда приходиться применять исскуственные приемы.
Логарифмические уравнения - решаются тремя методами, то есть переход от уравнения к уравнению - следствию;метод введения новых переменных логарифмирования, то есть переход от уравнения к уравнению.
А так же во многих случаях при решения логарифмического уравнения приходиться использовать свойства логарифма произведения, частного, степени, корня.
2 Виды неравенств в школьном курсе
В целом изучение неравенств в школьном курсе математики организовано так же, как и уравнений.
Отметим ряд особенностей изучения неравенств.
Как и в случае уравнений отсутствует теория равносильности неравенств. Учащимся предлагаются её незначительные фрагменты, приведённые в содержании учебного материала.
Большинство приёмов решения неравенств состоит в переходе от данного неравенства a>b к уравнению а=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Например, такая ситуация возникает при решении рациональных неравенств методом интервалов, при решении простейших тригонометрических неравенств.
В изучении неравенств большую роль играют наглядно - графические средства.
Два выражения (числовые или буквенные), соединённые одним из знаков: «больше» (>), «меньше» (<), «больше или равно» (≥), «меньше или равно» (≤) образуют неравенство (числовое или буквенное). Любое справедливое неравенство называется тождественным.
В зависимости от знака неравенства мы имеем либо строгие неравенства (> , <), либо нестроги (≥ , ≤).
Буквенные величины, входящие в неравенство, могут быть как известными, так и неизвестными.
Решить неравенство - это найти границы, внутри которых должны находиться неизвестные, так чтобы неравенство было тождественным.
Основные свойства неравенств:
Если a < b, то b > a; или если a > b, то b < a .
Если a > b, то a + c > b + c; или если a < b, то a + c < b + c. То есть, можно прибавлять (вычитать) одно и то же число к обеим частям неравенства.
Если a > b и c > d, то a + c > b + d . То есть, неравенства одного смысла (с одинаковым знаком > или <) можно почленно складывать.
Если a > b и c < d, то a - c > b - d . Или, если a < b и c > d, то a - c < b - d . То есть, неравенства противоположного смысла можно почленно вычитать одно из другого, и брать знак неравенства, являющегося уменьшаемым.
Если a > b и m > 0, то ma > mb и a/m > b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же положительное число. Неравенство при этом сохраняет свой знак.
Если a > b и m < 0, то ma < mb и a/m < b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же отрицательное число. Неравенство при этом меняет свой знак на обратный.
Неравенства, содержащие неизвестные величины, подразделяются на:
¾алгебраические;
¾трансцендентные;
Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени. Неравенство - алгебраическое, первой степени. Неравенство - алгебраическое, второй степени. Неравенство - трансцендентное. Виды неравенства и способы их решения: )Линейные неравенства Пример 5: Решить неравенство Ответ: x<-2. 2) Квадратные неравенства Пример 6: Решить неравенство х2> 4
х2> 4
(х - 2)∙(х + 2) > 0. Решаем методом интервалов.
) Рациональные неравенства Пример 7: Найти все целые значения, удовлетворяющие неравенству Методом интервалов:
Решение неравенства: Целые числа, принадлежащие интервалу: -6;-5;-4;1. Ответ:-6;-5;-4;1. 4) Иррациональные неравенства Начинать решение иррациональных неравенств нужно с нахождения области определения. Пример 8: Решить неравенство Область определения: Так как арифметический корень не может быть отрицательным числом, то Ответ: [-2;7)/ ) Показательные, логарифмические неравенства Пример 9: Решите неравенство.. Пример 10: Решите неравенство. Ответ:.
3 Особенности решения уравнения с параметрами
Рассмотрим уравнение
F(х,у,...,z;б,в,...,г)=0(1)
с неизвестными х, у, ..., z и с параметрами б,в, ..., г;при всякой допустимой системе значений параметров б0,в0, ..., г
0
уравнение (1) обращается в уравнение
F(х,у,...,z;б0,в0,...,г0)=0(2)
с неизвестными х, у,..., z, не содержащее параметров. Уравнение (2) имеет некоторое вполне определенное множество решений. Решить уравнение содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения. Основные виды уравнений с параметрами: ) Линейные и квадратные уравнения, содержащие параметр Линейные и квадратные уравнения, содержащие параметр, можно объединить в одну группу - группу уравнений с параметром не выше второй степени. Уравнения с параметром не выше второй степени являются самыми распространенными в практике итоговых и конкурсных заданий. Их общий вид определяется многочленом. Контрольные значения параметра определяются уравнением. На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов. Тогда решением всякого уравнения с параметром не выше второй степени осуществляется по следующим этапам: На числовой прямой отмечаются все контрольные значения параметра, для которых соответствующие частные уравнения не определены. На области допустимых значений параметра исходного уравнения при помощи равносильных преобразований приводится к виду. Выделяют множество контрольных значений параметра, для которых уравнение имеет конечное множество решений, то для каждого найденного контрольного значения параметра соответствующее частное уравнение решается отдельно. Проводится классификация частных уравнений по первым трем типам. На бесконечном множестве решений уравнения проводится решение уравнения, выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых и, соответствует третий тип не особых частных уравнений. Выделяются контрольные значения параметра, для которых дискриминант обращается в нуль. Соответствующие не особые частные уравнения имеют двукратный корень. Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков определяется знак дискриминанта. ) Дробно-рациональные уравнения, содержащие параметр, сводящиеся к линейным. Процесс решения дробно-рациональных уравнений протекает по обычной схеме: данное уравнение заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего учащиеся решают известным им способом целое уравнение, исключая посторонние корни, то есть числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы посторонние корни исключить, требуется находить значение параметра, обращающее общий знаменатель в нуль, то есть решать соответствующие уравнения относительно параметра. ) Иррациональные уравнения, содержащие параметр. Главными особенностями при решении уравнений такого типа являются: Ограничение области определения неизвестной х, так как она меняется в зависимости от значения параметра; При рассмотрении всех особых случаев и возведении обеих частей иррационального уравнения в квадрат мы переходим к решению квадратного уравнения с параметром. ) Показательные уравнения, содержащие параметр. Большинство показательных уравнений с параметрами сводится к показательным уравнениям вида: аf(x) = bg(х), где а>0, b>0.
Область допустимых значений такого уравнения находится как пересечение областей допустимых значений функций f(x) и g(х). Для решения уравнения аf(x) = bg(х) необходимо рассмотреть следующие случаи:
При а=b=1 решением уравнения аf(x) = bg(х) является область его допустимых значений D.
При а=1, b≠1 решением уравнения аf(x) = bg(х) служит решение уравнения g(х)=0 на области допустимых значений D.
При а≠1, b=1 решение уравнения аf(x) = bg(х) находится как решение уравнения f(х) = 0 на области D.
При а=b (а>0, а≠1, b>0, b≠1) уравнение аf(x) = bg(х) равносильно уравнению f(х) = g(х) на области D.
При а≠b (а>0, а≠1, b>0, b≠1) уравнение аf(x) = bg(х) тождественно уравнению (c>0, c≠1) на области D.
) Логарифмические уравнения, содержащие параметр. Решение логарифмических уравнений с параметрами сводится к нахождению корней элементарного логарифмического уравнения. Важным моментом решения уравнений такого типа является проверка принадлежности найденных корней ОДЗ исходного уравнения. Основные методы решения уравнений, содержащих параметр: Аналитический метод 4 Особенности решения неравенства с параметрами
Неравенство с параметрами - математическое неравенствовнешний вид и решение которого зависит от значений одного или нескольких параметров. Как при решении уравнения, так и при решении неравенства требуется найти все те значения неизвестной величины, для каждого из которых указанное соотношение оказывается верным. Решение неравенства (уравнения) может включать в себя несколько методов решения, соответствующих каждому виду уравнения при определенных значениях параметра. Например, при каком-то значении параметра неравенство линейное, поэтому решаем его аналитически тождественными преобразованиями; при остальных значениях параметра неравенство квадратичное, - решаем его функционально-графическим способом. Аналогично уравнениям с параметрами, неравенства с параметрами имеют ту же классификацию видов и методов решения. ) Линейные и квадратные неравенства, содержащие параметр ) Дробно-рациональные неравенства, содержащие параметр, сводящиеся к линейным. Решение некоторых дробно-рациональных неравенств сводится к решению неравенств первой или второй степени. ) Иррациональные неравенства, содержащие параметр. ) Показательные неравенства, содержащие параметр. ) Логарифмические неравенств, содержащие параметр. Основные методы решения неравенств, содержащих параметр: Аналитический метод Свойства функций в задачах, содержащих параметр. Функциональный подход. Графический метод. Координатная плоскость (x;y). Графический метод. Координатная плоскость (x;a).
Решение задач с параметрами является одним из самых трудных разделов школьной математики. При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить довольно разветвленные логические построения, аккуратность и внимательность для того, чтобы не потерять решений и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры, но, в свою очередь, эти задачи сами способствуют их развитию. Опыт вступительных экзаменов показывает, что учащиеся, владеющие методами их решения, обычно успешно справляются и с другими задачами. К сожалению, в программах по математике для неспециализированных школ задачам с параметром практически не отводится места, а, например, в учебнике для учащихся школ и классов с углубленным изучением курса математики («Алгебра и математический анализ для 10 и 11 классов», Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд) им отведено место только в 11-м классе. Между тем, задачи с параметрами можно и нужно использовать уже начиная с линейных и квадратных уравнений и неравенств. Это могут быть задачи нахождения решений в общем виде, определения корней, удовлетворяющих каким-либо свойствам, исследования количества корней в зависимости от значений параметра. Так сделано в «Сборнике задач по алгебре для 8-9 классов», 1994 г. (авторы: М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич). Важно, чтобы школьники уже на первых простых примерах усвоили: во-первых, необходимость аккуратного обращения с параметром - фиксированным, но неизвестным числом, поняли, что оно имеет двойственную природу (с одной стороны, это некоторое число, с другой стороны, степень свободы общения с ним ограничивается его неизвестностью); во-вторых, что запись ответа существенно отличается от записи ответов аналогичных уравнений и неравенств без параметра. Методически было бы правильно каждый пройденный тип уравнений (неравенств) завершать задачами с использованием параметра. Во-первых, школьнику трудно привыкнуть к параметру за два-три занятия - нужно время; во-вторых, использование подобных задач улучшает закрепление пройденного материала; в-третьих, оно способствует развитию его математической и логической культуры, а также развитию интереса к математике, поскольку открывает перед ним новые методы и возможности для самостоятельного поиска. Понятие параметра является математическим понятием, которое часто используется в школьном курсе математики и в смежных дисциплинах. класс - при изучении линейной функции и линейного уравнения с одной переменной. класс - при изучении квадратных уравнений. Общеобразовательная программа школьного курса математики не предусматривает решение задач с параметрами, а на вступительных к заменах в вузы и на ЕГЭ по математике задачи с параметрами присутствуют, решение которых вызывает большие затруднения учащихся.Задачи с параметрами обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности. При решении уравнения (неравенства) можно пользоваться следующим алгоритмом. Алгоритм решения уравнения или неравенства с параметром 1. Определяют ограничения, налагаемые на значения неизвестного и параметра, вытекающие из того, что функции и арифметические операции в или имеют смысл. Определяют формальные решения, записываемые без учета ограничений. Если при решении возникают контрольные значения параметра, то их наносят на числовую ось. Эти значения разбивают область допустимых значений параметра на подмножества. На каждом из подмножеств решают заданное уравнение.. Исключают те значения параметра, при которых формальные решения не удовлетворяют полученным ограничениям. На числовую ось. добавляют значения параметра, найденные в п.3. Для каждого из промежутков на оси. записывают все полученные решения в зависимости от значений параметра. (В случае достаточно простых уравнений п.4 можно опустить). Выписывают ответ, т.е. записывают решения в зависимости от значений параметра. Наличие параметра в задаче предполагает специальную форму записи ответа, позволяющую установить, каков ответ для любого допустимого значения параметра. Недопустимые значения также указываются в ответе, и считается, что при этих значениях параметра задача не имеет решения. При записи ответа обычно значения параметра перечисляются в порядке возрастания от −∞ до +∞, но иногда для компактности ответа объединяют промежутки для параметра, на которых формулы решения совпадают. В случае ветвления решения удобно использовать числовую прямую., на которую наносятся контрольные значения параметра, а на промежутках, на которые эти значения разбили прямую, указываются ответы задачи. Данный прием позволяет в дальнейшем не потерять найденные ответы и четко указать значения параметра, которым они соответствуют. Продемонстрируем сказанное выше на примере. Пример 10: Решить неравенство. Контрольные значения параметра получаются из условия, так как при неравенство не содержит переменной x. Нанесем на числовую ось Oa контрольные значения. Они разбивают ось Oa на промежутки: ) a<0; 2) 0< a <2; 3) a>2 На каждом из этих промежутков решим данное неравенство. Значения a=0 и. a=2 требуют отдельного рассмотрения. Если a<0, то a(a-2)>0. Разделив обе части неравенства на множитель a(a − 2) ≠ 0 , получим x>. Если 2>a>0, a(a − 2) < 0 и, следовательно, x<. Если a>2, a(a − 2) > 0 и x>/ Нанесем получаемые в ходе решения ответы на соответствующие промежутки числовой оси Oa и запишем ответ. Промежуток, к которому относится соответствующее решение, помечается на рисунке дугой. На ее конце ставится стрелочка в том случае, если это решение не относится к крайней точке промежутка.
Ответ: Если a<0, то x>; если 0 Главная особенность задач с параметрами - ветвления решения в зависимости от значений параметров. Другими словами, процесс решения осуществляется классификаций частных уравнений (неравенств) по типам с последующим поиском решений каждого типа. Одновременно решение бесконечной совокупности частных уравнений и неравенств с учетом требования равносильности преобразований возможно лишь при развитии достаточного уровня логического мышления. С другой стороны, формирование методов решения уравнений и неравенств с параметрами обеспечивает значительный процесс в развитии математической культуры учащихся. Развивающий характер уравнений и неравенств с параметрами определяется их способностью реализовывать многие виды мыслительной деятельности учащихся: Выработка определенных алгоритмов мышления. Умение определить наличие и количество корней в уравнении. Решение семейств уравнений, являющихся следствием данного. Выражение одной переменной через другую. Повторение большого объема формул при решении. Значение соответствующих методов решения. Широкое применение словесной и графической аргументации. Развитие графической культуры учащихся. Все вышесказанное позволяет говорить о необходимости изучения решений задач с параметрами. уравнение неравенство параметр
Заключение
Таким образом, в нашей курсовой работе речь шла о уравнениях и неравенствах с параметрами в школьном курсе математике, особенности их решения. Были рассмотрены уравнения и неравенства в школьном курсе математике, особенности решения уравнений и неравенств с параметрами.Была разработана методики к решению уравнений и неравенств с параметрами. Цель нашей курсовой работы заключалась в выявление видов, методов решения уравнений и неравенств с параметрами. Для достижения данной цели, была подобрана и изучена литература по данной проблеме, исследовано особенности решения уравнений и неарвенств с параметрамишкольном курсе математики основной школы, представлена методические рекомендации к решению уравнений(неравенств) с параметрами. Вывод: Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты. В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано. Изучение уравнений и неравенств с параметрами в общеобразовательных школах дает учащимся большие возможности для анализа различных ситуаций, то есть показывает значимость этих понятий при решении многих практических задач. Именно с простейших практических задач и приложений математически постепенно формируется у школьников понимание значимости математики в жизни.
Список используемой литературы уравнение неравенство математика 1.Алгебра. 7 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2010. 2.Алгебра. 7 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2010. 3.Алгебра. 7 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011. Алгебра. 8 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2012. Алгебра. 8 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2011. Алгебра. 8 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011. Алгебра. 9 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2013. Алгебра. 9 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2013. Алгебра. 9 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011. Алгебра. Учеб.для 7 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2011. Алгебра. Учеб.для 7 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2012. Алгебра. Учеб.для 8 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2014. Алгебра. Учеб.для 8 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2011. Алгебра. Учеб.для 9 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2010. Алгебра. Учеб.для 9 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2001. Беляева Э.С. Математика. Уравнение и неравенство с параметрами в 2 ч.: Учебное пособие/ Беляева Э.С., Потапов А.С., Титоренко С.А. -., - М.:,2009. Крамор В.С. Задачи с параметром и методы их решения: Учебное пособие /- М.: Оникс; Мир и Образование,2007 Козко А.И. Задачи с параметрами и другие сложные задачи: Учебное пособие для вузов/Козко А. И.,Чирский В. Г. - М.:,МЦНМО,2007. Мирошин В.В. Решение задач с параметрами. Теория и практика: Учебное пособие /. - М.: Экзамен,2009. Прокофьев А.А. Задачи с параметрами: Учебное пособие. - М.: МИЭТ, 2004. Севрюков П.Ф. Школа решения задач с параметрами: Учебное пособие /Севрюков П.Ф., Смоляков А. Н.-2-е изд.- М.:,2009.